This work proposes a hybrid intelligent framework for UAV pursuit missions that can be deployed in both single- and multi-agent scenarios by integrating deep reinforcement learning and fuzzy logic. Fuzzy rules are incorporated into both the yaw-control module and the DRL reward function to enhance fault tolerance, particularly in the presence of sensor noise, packet loss, and other disturbances commonly encountered in real flight operations. The proposed method is validated through a three-stage evaluation pipeline, including pure MATLAB/Simulink simulations, ROS2/Gazebo simulations with a realistic physics engine, and in-field flight experiments. The simulation and experimental results collectively demonstrate the effectiveness and safety of the proposed algorithm.

How to use

The main simulation tool Bingze_swarm_2v2 folder -> chase2.m, this file creates the MATLAB simulation environment with randomized located interceptors and intruders, where interceptors are equipped with well-trained RL agent (TrainedAgent_1v1_2).

The following code snippet creates the RL environment and load the pre-trained agent:

mdl = "chasing2";

Tfinal = 25;

sampleTime = 0.1;

agentBlk = ["chasing2/Agent","chasing2/Agent1"];

obsInfo = rlNumericSpec([23 1]);

numObservations = obsInfo.Dimension(1);

numActions = 4;

actInfo = rlNumericSpec([numActions 1],...

    "LowerLimit",-1,...

    "UpperLimit",1);

env = rlSimulinkEnv(mdl,agentBlk,{obsInfo,obsInfo},{actInfo,actInfo});

env.ResetFcn = @(in)chasingReset2(in);

env.UseFastRestart = "Off";

rng(0)

%% =============================================================================

doTraining = false; % Toggle this to true for training. 

if doTraining

    % Train the agent

    trainingStats = train(Agent2,env,trainOpts);

else

    % Load pretrained agent for the example.

    load TrainedAgent_1v1_2 Agent2

    Agent3 = Agent2;

End

Version: MATLAB version 2024a

Please follow the steps to run the simulation:

1. open 'chase2.m' and 'chasing2.slx'

2. load the fuzzy logic model to workspace 'fis4.fis' (you can also use Fuzzy Logic Designer App)

3. run the .m file section by section.

4. run the .slx file.

features:

1. During training, the initial position and orientation of the ownship(blue UAV) is randomized.

2. if you modify the initial position of the ownship (within 25m of the intruder), retraining is not required.

3. you can also change the predefined route of the intruder aircraft and tune its speed.

Dataset Details

This part includes simulation and experiment results in MATLAB/Simulink; ROS2/Gazebo and in-field tests.

Matlab/Simulink

The following figures illustrate the initial layout of the interception scenario featuring two ownships and two intruder aircraft in Matlab/Simulink, as well as the interception results with trajectories (perspective view and top view).

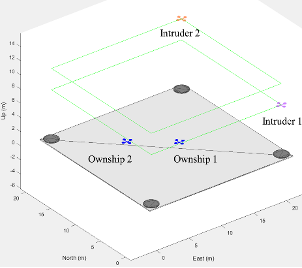
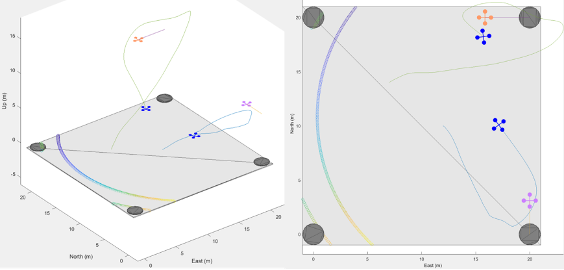
ROS2/Gazebo

As shown in Figure 7, the no-fly zone represents the area that's enclosed within the white box. The two intruder UAVs entered the designated no-fly zone and were subsequently detected by the ownship UAVs, which then initiated the interception process. Similarly, a successful interception is defined as the condition where the Euclidean distance between an ownship and its assigned target is reduced to 2 meters. Once intercepted, both the target UAV and the ownship will hover at the capture location, awaiting the successful interception of all intruders to terminate the simulation. Figures 8 and 9 depict the Euclidean distances between each ownship and its corresponding intruder aircraft, along with the specific coordinate errors on each axis. It is noteworthy that both ownships completed the task in approximately 15 seconds, well within the 30-second time constraint set for the mission.

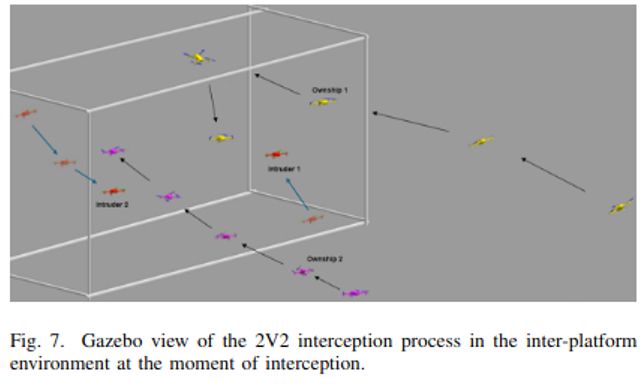
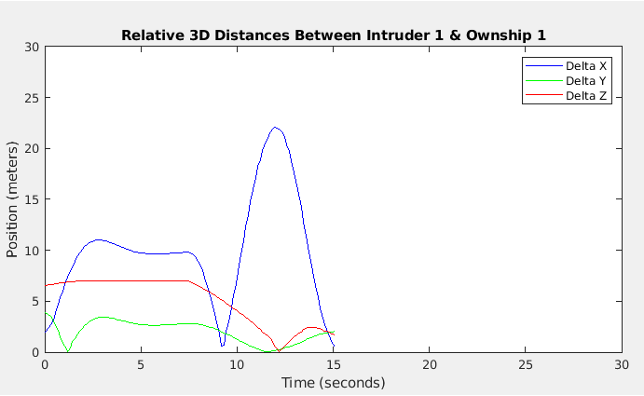
Figure 8a: Coordinate Errors between Own ship 1 & Intruder 1

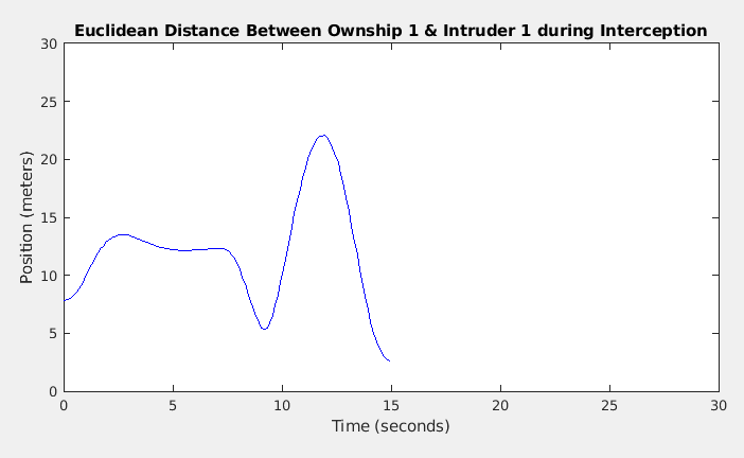
Figure 8b: Euclidean Distance between Own ship 1 & Intruder 1

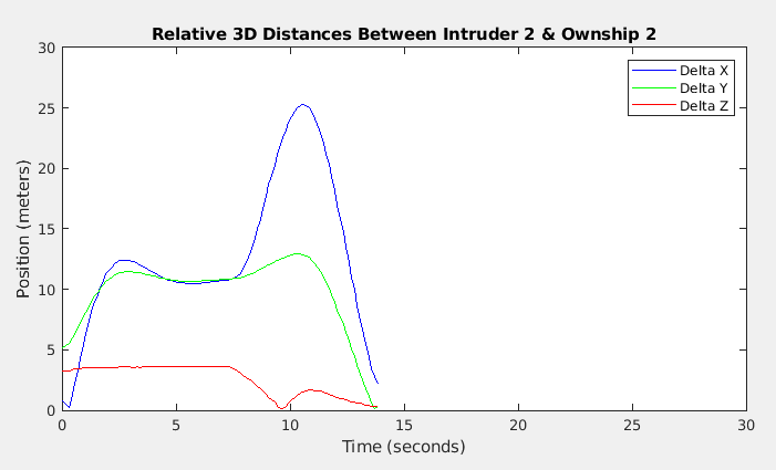
Figure 9a: Coordinate Errors between Own ship 2 & Intruder 2

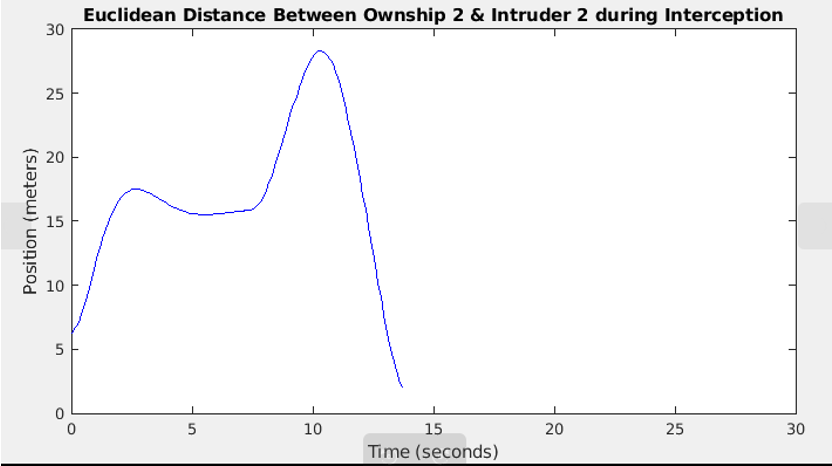
Figure 9b: Euclidean Distance between Own ship 2 & Intruder 2

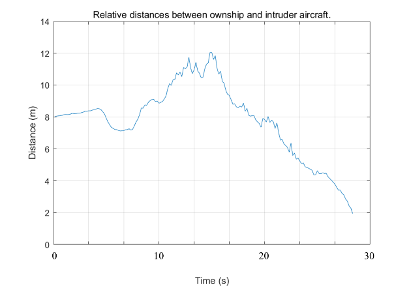
In-field flight test

The following figures demonstrate a real interception case with one interceptor and one intruder UAV, the line figure depicted that the Euclidean distance between two drone is converged to 2 meters (a preset threshold).

Reference

@inproceedings{xia2025icuas,
  title  = {"Synthesized Control for In-Field UAV Moving Target Interception Via Deep Reinforcement Learning and Fuzzy Logic"},
  author       = {"Xia, Bingze and Akhlaque, M. A. and Mantegh, Iraj and Bolic, Miodrag and Xie, Wenfang"},
  booktitle    = {"2025 International Conference on Unmanned Aircraft Systems (ICUAS)"},
  year         = {2025},
  organization = {"IEEE"},
  pages        = {1109--1116},
  month        = {May}
}